Realtime Rendering笔记 04变换（上）

这一章主要是数学知识，这个部分具体推导过程会省略掉一大半，直接贴个结论。感兴趣的可以看看原文。满足下面两个公式的是线性变换：

$f (x) + f (y) = f (x + y)$

$k f (x) = f (k x)$

仿射变换：4×4矩阵（线性+平移）

表示向量： $v = (v_{x} v_{y} v_{z} 0)^{T}$

表示点： $v = (v_{x} v_{y} v_{z} 1)^{T}$

4.1 基础变换

这一小节会包含以下几个变换矩阵

名称	名称	特点
T(t)	平移矩阵（translation matrix）	移动点，仿射变换
Rx(ρ)	旋转矩阵（rotation matrix）	围绕x轴进行旋转，同样的也有围绕y和z旋转的矩阵，仿射变换
S(s)	缩放矩阵（scaling matrix）	旋转矩阵，仿射变换
Hij (s)	切变矩阵（shear matrix）	将向量 i 沿向量 j 的方向剪切一个因子s。i, j ∈ {x, y, z}。仿射变换。
E(h, p, r)	欧拉变换（Euler transform）	由欧拉角航向角（偏航角）、俯仰角和翻滚角给出的方向矩阵。正交且仿射。
Po(s)	正交投影（orthographic projection）	将物体平行投影到某个平面或体积上。仿射变换。
Pp(s)	透视投影（perspective projection）	将物体透视投影到某个平面或体积上。
slerp(ˆq, ˆr, t)	球面插值（slerp transform）	根据四元数ˆq和ˆr以及参数t，创建一个插值四元数。

4.1.1 平移矩阵

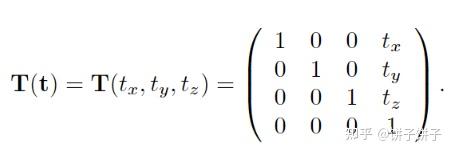
逆矩阵： $T^{- 1} (t) = T (- t)$

4.1.2 旋转矩阵

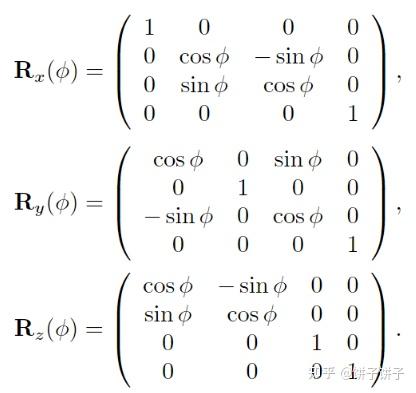
逆矩阵： $R_{i}^{- 1} (φ) = R_{i} (- φ)$

4.1.3 缩放矩阵

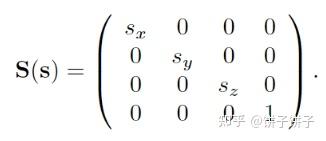
逆矩阵： $S^{- 1} (s) = S (1 / s x, 1 / s y, 1 / s z)$

直接缩放S：

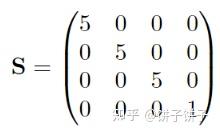
齐次坐标缩放S’：

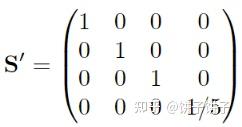
齐次坐标缩放开销要大一点，因为总是涉及到除法运算

反射矩阵：

当缩放因子的一个或3个分量为负值时就是反射矩阵（reflection matrix）或者镜像矩阵（mirror matrix）
如果两个分量为-1，会导致一个π弧度的旋转
反射矩阵与旋转矩阵结合仍是反射矩阵

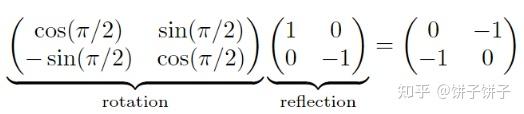
判断三角形的正反朝向是需要看绕序的，如果经过反射矩阵变换的话，可能会导致绕序反向，从而导致光照错误。那么如何判断是否进行了反射矩阵变换呢？看行列式就可以了，行列式是-1说明存在反射矩阵

定向缩放：

如果我们沿着标准坐标系x、y、z坐标系变换的话，那缩放是很简单的事情。假如我们需要让缩放沿着任意方向缩放怎么办呢？这个时候需要构造一个复合矩阵。

1. 构造一个变换矩阵 F ，用于把标准坐标系变换到某个想要缩放的方向：

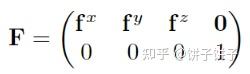
2. 在新坐标系中应用标准缩放矩阵 S

3. 由于 F 是正交矩阵，所以它的逆矩阵就是它的转置矩阵。用 FT 变换回原始坐标

4. 最终的复合矩阵： $X = F S (s) F^{T}$

4.1.4 斜切变换

特点就是改变对象的形状但是不改变体积有6种基本形式： $H_{x y} (s), H_{x z} (s), H_{y x} (s), H_{y z} (s), H_{z x} (s), H_{z y} (s)$

以 $H_{x z} (s)$ 为例，会发生这种变换

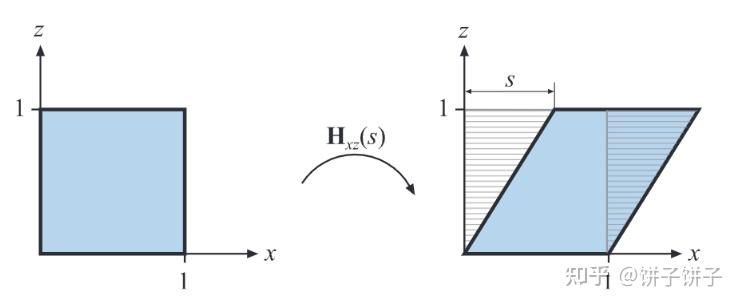
公式：

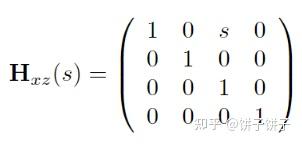
可以把一个 $(p_{x}, p_{y}, p_{z}, 1)^{T}$ 的点变成 $(p_{x} + s p_{z}, p_{y}, p_{z}, 1)^{T}$

更通用的公式：

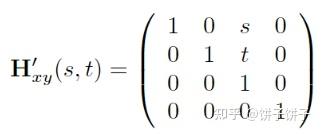
此时的x受s影响，y受t影响

这个公式其实就是 $H'_{i j} (s, t) = H_{i k} (s) H_{j k} (t)$

换言之 $H'_{x y} (s, t) = H_{x z} (s) H_{y z} (t)$

4.1.5 变换的级联

矩阵不满足乘法交换律！！！变换顺序很重要！！！

变换的级联就是将多个变换矩阵依次相乘，以实现一系列连续的变换操作。为啥呢？因为结合到一起之后能减少计算机运算，省性能。

4.1.6 刚体变换

刚体变换就是不改变形状的变换，比如打篮球，篮球旋转又平移（假设没有拍扁）

所以刚体变换就是旋转+平移。

先旋转后平移

对物体进行刚体变换需要先旋转后平移。公式：

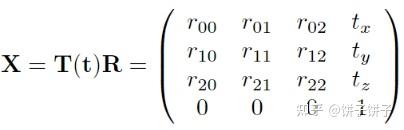
旋转矩阵可以写成这样：

整个公式可以写成这样：

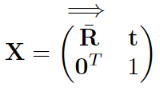
逆矩阵：X-1 = (T(t)R)-1 = R-1T(t)-1 = RTT(-t) 也可以写成这样：

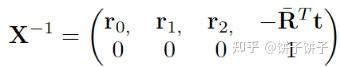
先平移后旋转

那有没有先平移后旋转的情况呢？摄像机看啥都是反过来的，所以摄像机就是先平移后旋转。咋构建摄像机的刚体变换矩阵呢？看这个图：

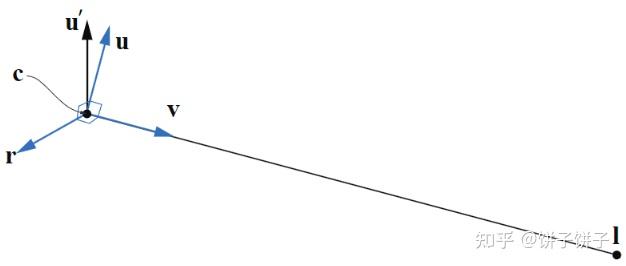
摄像机咋表示？我们需要算出来摄像机的三个基向量。咋算呢？

c：摄像机位置

l：目标位置

那我们很容易把v算出来，就是c-l

接下来我们构建一个u’：绝对向上的方向，也就是(0, 1, 0)

我们再加个向右的方向r，那么r能够通过v x u’算出来，然后进行一下归一化

然后我们就可以算出相机真正的向上方向了，通过r x v （有没有觉得有点像billboard的计算呢？）

算好之后执行先平移再旋转的操作就好了：

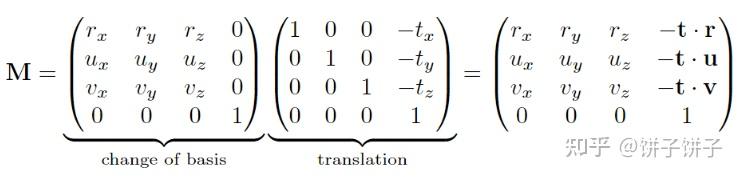
4.1.7 法线变换

这里很多地方都推导过，大家应该很熟悉，所以我直接贴结论当复习了：

在仅包含平移、旋转和均匀缩放的情况下，可以直接使用原始矩阵进行法线变换，并根据需要进行归一化
存在非均匀缩放时，使用转置伴随矩阵或者转置逆矩阵。

4.1.8 逆矩阵的计算

如果矩阵是一个单一变换或者是一系列具有给定参数的简单变换的序列，那么可以通过“反转参数”和矩阵顺序来轻松计算矩阵的逆。例如，如果 $M = T (t) R (ϕ)$ ，那么 $M^{- 1} = R (- ϕ) T (- t)$ 。
正交矩阵的逆矩阵是它的转置矩阵
啥也不知道的话，用伴随矩阵法、克拉默法则、LU分解、高斯消元法算。

4.2 特别的矩阵运算和操作

4.2.1 欧拉角

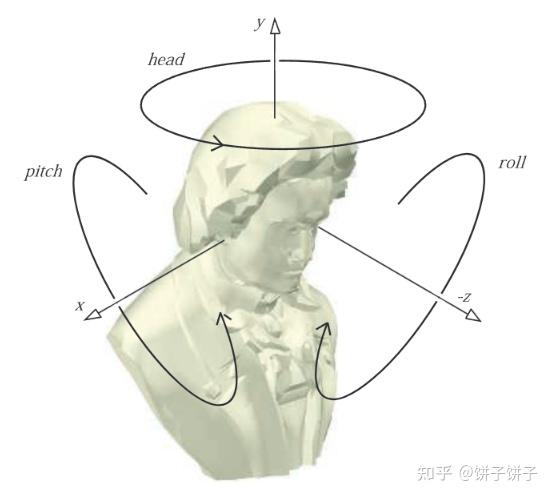
来看这张图，把它背下来。有三个方向，分别是pitch、head、roll。这里就不翻译了，因为公式里总出现phr三个字母。

它的表达式是： $E (h, p, r) = R_{z} (r) R_{x} (p) R_{y} (h)$

它的转置矩阵可以表示其逆： $E^{- 1} = E^{T} = (R_{z} R_{x} R_{y}) T = R_{y}^{T} R_{x}^{T} R_{z}^{T}$

向上方向有两种主流，y-up或者z-up

欧拉角之间的插值并非简单逐角度插值，且可能存在多个欧拉角表示相同的方向 可能会有万向节锁，即某些角度组合会丢失一个自由度，导致旋转无法精确表示，四元数等其他方法能解决欧拉角的一些缺陷

4.2.2 从欧拉变换中提取参数

欧拉角的推导有点点麻烦，而且一般最后是直接用结论的，简单讲一下大概思路。我们构建一个3×3的矩阵（通常是4×4的变换矩阵，但是我们先忽略最后一行和最后一列）

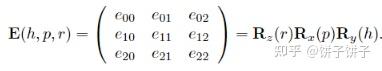
前面讲过旋转矩阵的公式，分别把xyz三个方向旋转矩阵代进去乘，乘完之后就得到一个很恶心的公式

然后去找里面比较特殊的值，比如第三行第一列的E31第三行第三列的E33挺特殊对吧？把他们除掉，就得到了：

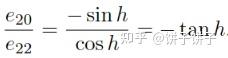
(这里的图是这样是因为书上是从0开始算的，大家知道哪个是哪个就好）

然后又用 $E_{12} / E_{11}$ 求出-tanr，然后 $E_{32}$ 本来就挺特殊的，直接就是sinp

最后我们就得到了三个参数：

$h = a t a n 2 (- E 31, E 33)$

$p = a r c s i n (E 32)$

$r = a t a n 2 (- E 12, E 22)$

（明明想讲个大概思路来着，一不留神就讲完了<(￣︶￣)↗）

把那个很恶心的矩阵拎出来，会发现如果 $c o s p = 0$ （也就是p是90°、-90°）时，公式就变成了这样：

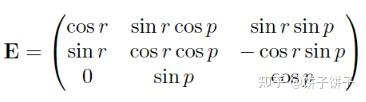
$E_{31}$ （ $e_{20}$ )消失了！！！那求不了h了啊？？所以就丢失自由度喽(￣▽￣)╭ Ohnooooo…..

那r还有的救吗？当然有，你看把第二行第一列除以第一行第一列（ $E_{21} / E_{11}$ ）不就又有r了吗？

xyz用于建模系统 zxy用于动画 zxz在某些应用中更优，因为不会发生万向节锁

4.2.3 矩阵分解

这里书上也没咋讲，大家感兴趣就去看看里面列的文献吧~

（浅墨大佬更新过real time rendering里面的所有文献链接）

很简单的办法：

平移：找4×4的最后一列

反射：查行列式是否为负数

4.2.4 绕任意轴旋转

（碎碎念：怎么还有怎么还有）

不仅有，还有3种方法！

方法1

用一个变换矩阵变换到标准坐标系（旋转矩阵M）
执行旋转（使用矩阵 $R_{x} (ɑ)$ ）
变换回原坐标系（应用矩阵 $M^{- 1}$ ）（其实和之前讲的定向缩放是差不多的思想）

看下图就懂了

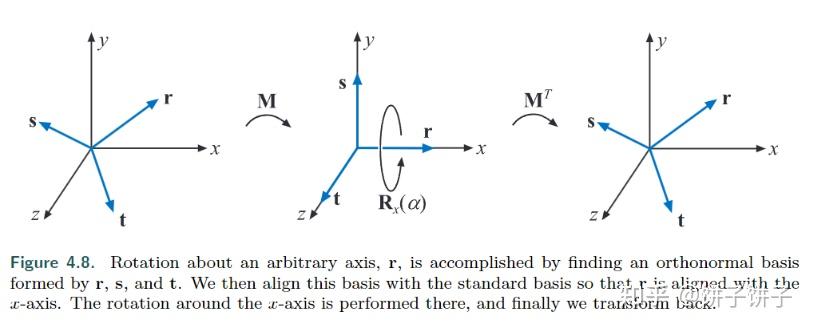
咋求M！！！！咋求啊！！！！算求（不是

我们又又又又又构建正交基 r, s, t。

看上图，假设我们是绕着r旋转了一个ɑ的情况下：

求r：直接把r变到x轴

求s：找到r中绝对值最小的分量，设为0，剩余两个分量交换位置，并对一个取负值；然后再对生成的向量归一化。也就是这样：

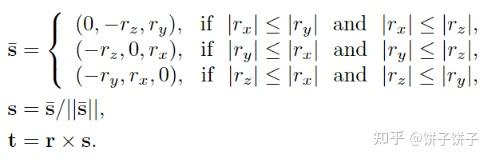
求t： $t = r \times s$ 于是我们终于得到了三个正交基，就可以构造矩阵了

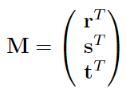
（碎碎念：这个方法怎么和立方体投影找光线的方法有点像啊）

方法2

有好人直接给了个矩阵，拿去用吧！

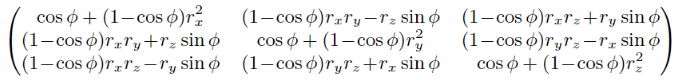
方法3

四元数，这个内容太多了我们放在下一节说。

4.3 四元数

这部分不懂的可以看三蓝一棕理解下。三言两语讲不清楚，我就直接贴结论了。

4.3.1 四元数数学基础

定义

知乎的语法和我自己笔记的语法不太一样，q上面的波浪线大家就当成四元数的符号^好了

$\tilde{q} = (q_{v}, q_{w}) = i q_{x} + j q_{y} + k q_{z} + q_{w} = q_{v} + q_{w} = s i n φ u_{q} + c o s φ q_{v} = i q_{x} + j q_{y} + k q_{z}$

其中 $i^{2} = j^{2} = k^{2} = - 1 ， j k = - k j = i, k i = - i k = j, i j = - j i = k$

四元数的基本运算

加法： $\tilde{q} + \tilde{r} = (q_{v}, q_{w}) + (r_{v}, r_{w}) = (q_{v} + r_{v}, q_{w} + r_{w})$

共轭： $\tilde{q} = (q_{v}, q_{w}) = (- q_{v}, q_{w})$

模长： $n (\tilde{q}) = \sqrt{q q *} = \sqrt{q * q} = \sqrt{q_{v} q_{v}} + \sqrt{q_{w}^{2}} = \sqrt{q_{x}^{2}} + \sqrt{q_{y}^{2}} + \sqrt{q_{z}^{2}} + \sqrt{q_{w}^{2}}$

乘法：

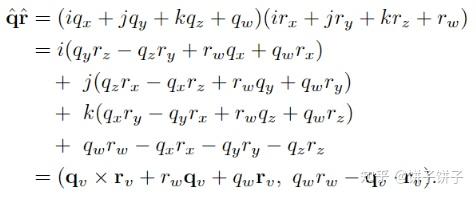
运算性质

共轭规则

$({\tilde{q}}^{*})^{*} = \tilde{q}$

$(\tilde{q} + \tilde{r})^{*} = {\tilde{q}}^{*} + {\tilde{r}}^{*}$

$(\tilde{q} \tilde{r})^{*} = {\tilde{r}}^{*} {\tilde{q}}^{*}$

模长规则

$n ({\tilde{q}}^{*}) = n (\tilde{q})$

$n (\tilde{q} \tilde{r}) = n (\tilde{q}) n (\tilde{r})$

乘法规则
- 线性性：

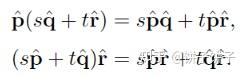
- 结合性：

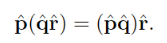
定义： $\tilde{q} = (q_{v}, q_{w})$ ，其中 $n (\tilde{q}) = \sqrt{\tilde{q}} = s i n φ u_{q} + c o s φ$ ，其中φ是旋转角度，uq是归一化旋转轴，满足|uq| = 1

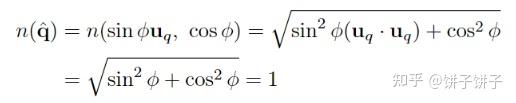
4.3.2 四元数的变换

（四元数一般是用在动画上的）

给定一个单位四元数 $\tilde{q} = (s i n φ u_{q}, c o s φ)$ ，其中 $u_{q}$ 是旋转轴的单位向量， $φ$ 是旋转角的一半。

一个点或者向量 $p = (p_{x}, p_{y}, p_{z}, 0)^{T}$ 可以拓展为四元数 $\tilde{p}$

旋转操作： ${\tilde{p}}^{'} = \tilde{q} \tilde{p} {\tilde{q}}^{- 1}$ (其中 ${\tilde{q}}^{- 1} = {\tilde{q}}^{*}$ )

旋转复合： ${\tilde{p}}^{″} = (\tilde{r} \tilde{q}) \tilde{p} ({\tilde{q}}^{- 1} {\tilde{r}}^{- 1}) = \tilde{c} \tilde{p} {\tilde{c}}^{- 1}$

四元数到矩阵的转换

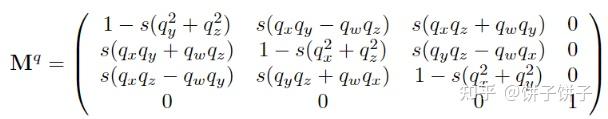
对于单位四元数可以简化成下列公式：

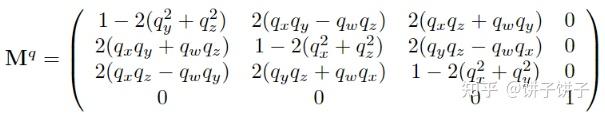
推导思路：先算 $\tilde{q} \tilde{p} {\tilde{q}}^{- 1}$ （用前面的乘法规则算），主对角线元素对应x, y, z轴分量，非对角线元素表示叉乘引入混合项。这里就不细说了，毕竟到最后只会把结论拿过去用。感兴趣的可以后面自己看看。

从矩阵到四元数的逆转换：这个推导起来更麻烦一点，直接贴结论

先求矩阵轨迹 $t r (M^{q})$

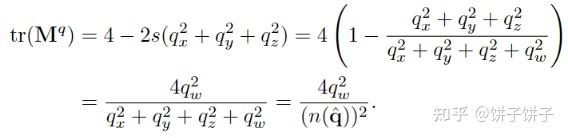
结果：

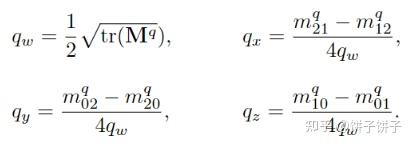
需要注意，要保证数值稳定，避免除以小数。

首先设置 $t = q_{w}^{2} - q_{x}^{2} - q_{y}^{2} - q_{z}^{2}$

然后计算 $m_{00} = t + 2 q_{x}^{2}, m_{11} = t + 2 q_{y}^{2}, m_{22} = t + 2 q_{z}^{2}$

计算 $u = m_{00} + m_{11} + m_{22} = t + 2 q_{w}^{2}$ 通过比较 $m_{00}, m_{11}, m_{22}, u$ 来确定哪个分量最大

如果 $u$ 最大（即 $q_{w}$ 最大），用这个公式

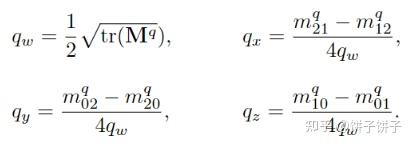
否则用这个公式：

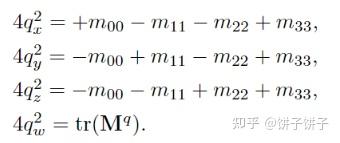
球面线性插值

希望到这里没有累倒（反正我要写倒了球面插值用来干啥呢？刚才说过欧拉角有个问题，就是不是插值旋转。但是球面插值可以。

SLERP的基本公式：

$s (\tilde{q}, \tilde{r}, \tilde{t}) = (\tilde{r} \tilde{q} - 1) t \tilde{q} = s l e r p (\tilde{q}, \tilde{r}, t) = s i n (φ (1 - t)) s i n φ \tilde{q} + s i n (φ t) s i n φ \tilde{r}$

qˆ和rˆ分别是两个四元数 φ是两个四元数的夹角

$c o s φ = q_{x} r_{x} + q_{y} r_{y} + q_{z} r_{z} + q_{w} r_{w}$

qˆ和rˆ的插值点位于四维单位球体上，四维单位球面是由所有满足 $q_{x}^{2} + q_{y}^{2} + q_{z}^{2} + q_{w}^{2} = 1$ 的四元数 $\tilde{q} = (q_{w}, q_{x}, q_{y}, q_{z})$ 组成的集合。对于参数t∈[0,1]，SLERP函数计算出一系列插值四元数，这些四元数共同构成从q^（当t=0时）到r^（当t=1时）的四维单位球面上的最短弧线。这个最短弧线位于由q^、r^和原点构成的平面与四维单位球面相交形成的圆上。这个圆是四维空间中的一个二维子空间，类似于三维空间中平面与球面相交形成的圆。

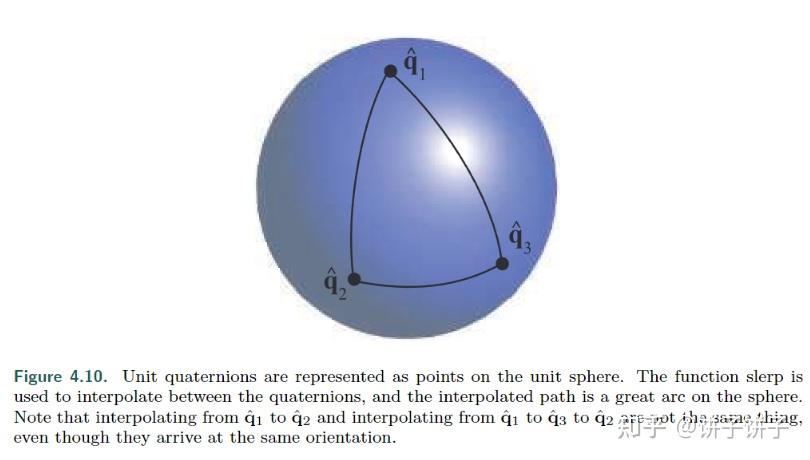
计算出的旋转四元数围绕一个固定的轴以恒定速度旋转。所以在插值过程中，旋转的速度是均匀的，不会出现加速或减速的情况。像SLERP这样的曲线，具有恒定速度且加速度为零，被称为测地线曲线。测地线是球面上两点之间的最短路径，类似于平面上的直线。在球面上，大圆是通过原点的平面与球面相交形成的圆。大圆上的弧线称为大圆弧。SLERP生成的最短弧线就是大圆弧的一部分。

球面插值，好。但是有个问题，直接插值计算的话要调用三角函数，计算量很大，所以有一些优化方法。比如可以把插值计算放到渲染管线里；增量；使用加法和乘法优化等等。这里感兴趣可以找文献看。

SQUAD

更好的插值办法是用SQUAD。这种方法需要在两个四元数 ${\tilde{q}}_{i}$ 和 ${\tilde{q}}_{i} + 1$ 之间引入两个额外的四元数 ${\tilde{a}}_{i}$ 和 ${\tilde{a}}_{i} + 1$ ，计算公式如图。

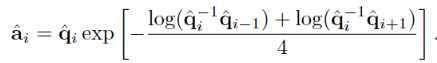
然后用SQUAD公式算

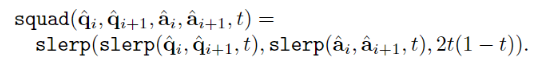
这个公式通过两次使用SLERP来构建，一次用于 ${\tilde{q}}_{i}$ 和 ${\tilde{q}}_{i} + 1$ 之间的插值，另一次用于 ${\tilde{a}}_{i}$ 和 ${\tilde{a}}_{i} + 1$ 之间的插值，然后再次使用SLERP将这两个结果结合起来

从一个方向s到另一个方向t的旋转

首先，归一化方向向量s 和t。

计算单位旋转轴 $u ： u = s \times t / ∣ s \times t ∣$

计算点积 $e = s \cdot t = c o s (2 φ)$ （2φ是s和t之间的夹角）

计算叉积的模 $∣ s \times t ∣= s i n (2 φ)$

$\tilde{q} = (s i n φ u, c o s φ)$

通过三角恒等式和半角公式算qˆ：

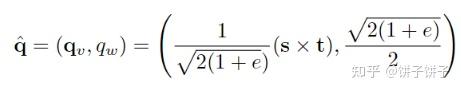
变成矩阵：

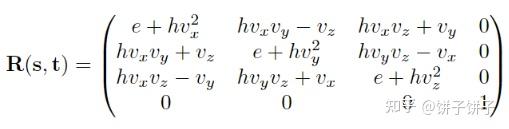
$v = s \times t$ 是旋转轴

如果s和t平行则直接返回 $\tilde{q} = (0, 1)$

$s \cdot t = - 1$ 时，取任意不平行于s的向量v，计算 $u = s \times v$

总算结束了~下半章我们再见。（嗝屁了